CRC校验与模2除法

CRC校验及其原理

CRC即循环冗余校验码（Cyclic Redundancy Check ）：是数据通信领域中最常用的一种查错校验码，其特征是信息字段和校验字段的长度可以任意选定。循环冗余检查（CRC）是一种数据传输检错功能，对数据进行多项式计算，并将得到的结果附在帧的后面，接收设备也执行类似的算法，以保证数据传输的正确性和完整性。基本原理是：在K位信息码后再拼接R位的校验码，整个编码长度为N位，因此，这种编码也叫（N，K）码。

CRC数据块的表示方法

任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应。例如：代码1010111对应的多项式为 $$ x^6 + x^3 + x^2+1 $$ 而多项式 $$ x^5 + x^3 + x^2+1 $$ 对应的代码101111。 10110101可以看作是 $$ 2^7 + 2^5 + 2^4+2^2+2^0 $$ 其表示式是从0开始的，所以其对就的CRC公式为： $$G(X)=x^7 + x^5 + x^4+x^2+1$$

模2除法

“模2除法”与“算术除法”类似，但它既不向上位借位，也不比较除数和被除数的相同位数值的大小，只要以相同位数进行相除即可。模2除法，使用的是异或运算。其逻辑表示为：

1^1=0
0^0=0
1^0=1
0^1=1

口决：同为0异为1

计算示例

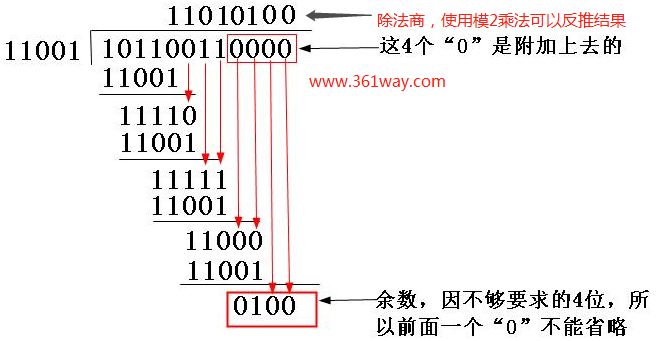
CRC校验的关键是如何求出余数，也就是校验码（CRC校验码），下面以一个例子来具体说明整个过程。现假设选择的CRC生成多项式为

$$G(X) = x^4+x^3+1$$

要求出二进制序列10110011的CRC校验码。

先把生成多项式转换成二进制数，由上面的表达式，可以得出被除数是5位（总位数等于最高位的幂次加1，即4+1=5 ，也可以看作第从0位开始的，到第4位就是5），很快就可得到表达式的二进制比特串为11001；

因为生成多项式的位数为5，得知CRC校验码的位数为4（校验码的位数比生成多项式的位数少1）；

计算过程如下：

把上步计算得到的CRC校验0100替换原始帧101100110000后面的四个“0”，得到新帧101100110100。再把这个新帧发送到接收端；

当以上新帧到达接收端后，接收端会把这个新帧再用上面选定的除数11001以“模2除法”方式去除，验证余数是否为0，如果为0，则证明该帧数据在传输过程中没有出现差错，否则出现了差错。

总结

模2除法的运算口决：先在信息码字的后面补齐最高幂次个0，再除以生成式的二进制格式，待余数位刚好等于最高幂次时，计算结束，得到的余数就是校验码。如：表达式的最高幂次为x^4，则补4个0，最后得的余数位是4位。

参考页面：最通俗的CRC校验原理剖析

捐赠本站(Donate)

如您感觉文章有用，可扫码捐赠本站！(If the article useful, you can scan the QR code to donate))